Hoe stabiel zijn bouwprofielen?

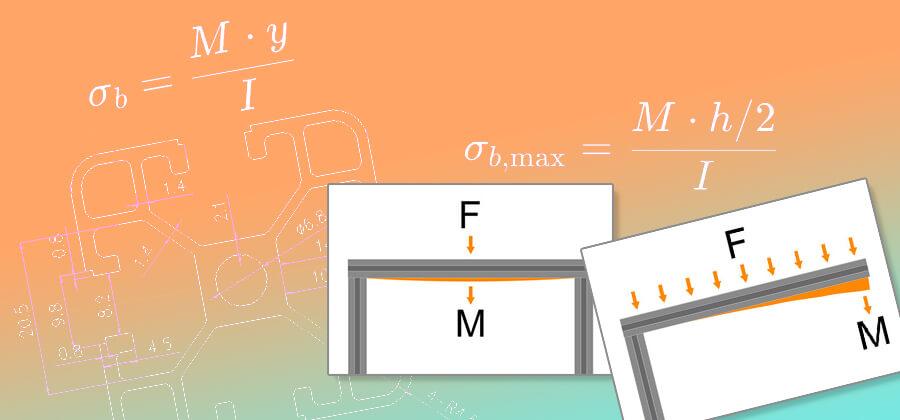
Stap voor stap wordt uitgelegd hoe je kunt berekenen of een constructieprofiel een belasting kan dragen of er blijvend onder zal vervormen.

Wanneer leidt een belasting tot permanente vervorming?

Het is volkomen logisch dat een constructieprofiel doorbuigt onder belasting. De mate waarin deze doorbuiging optreedt hangt grotendeels af van het profiel en de lengte ervan, het eigen gewicht, het extra gewicht, de verdeling van de belasting en het type montage. Op het eerste gezicht lijken de formules voor het berekenen van doorbuiging erg ingewikkeld. Daarom hebben we een aparte blogpost aan dit onderwerp gewijd, waarin we elke afzonderlijke parameter en de berekening in kleine, begrijpelijke stappen uitleggen. Maar wanneer is deze belasting te hoog? Wanneer beïnvloedt het gewicht permanente vervorming? We zullen deze vraag in detail behandelen in dit artikel.

Eerst een beetje theorie over buigspanning

Om de buigspanning te berekenen, d.w.z. de spanning die mechanisch op het materiaal inwerkt als gevolg van belasting, moeten we weten hoe sterk het materiaal is. Het helpt om naar het gegevensblad van het materiaal te kijken, omdat we de waarde van de vloeigrensR_e moeten bepalen (die ook wel vloeispanning of rekgrens wordt genoem). Dit kan van materiaal tot materiaal sterk verschillen. Zelfs bij een constructieprofiel van aluminium is een nadere beschouwing belangrijk, omdat niet al het aluminium hetzelfde is. De specifieke legering is hier belangrijk om de rekgrens te bepalen.

De rekgrens van een materiaal beschrijft de spanning waarbij het plastisch vervormt, bijvoorbeeld wanneer het materiaal permanent begint te vervormen zonder terug te keren naar zijn oorspronkelijke vorm wanneer de belasting wordt weggenomen. Het is daarom een belangrijke mechanische eigenschap die aangeeft hoeveel spanning een materiaal kan verdragen voordat het permanent begint te vervormen en wordt, net als de elasticiteitsmodulus, uitgedrukt in pascal of N/mm², een andere belangrijke fysische grootheid. Voor aluminium markeert de rekgrens het punt waarop elastische vervorming (die omkeerbaar is) overgaat in plastische vervorming (die onomkeerbaar is). Dit betekent dat als de rekgrens wordt overschreden, het aluminium profiel blijvende vervorming zal ondergaan door uitrekking. Onze constructieprofielen zijn gemaakt van een hoogwaardige EN AW 6063 T5 aluminiumlegering met een ongelooflijke vloeigrens van 292 MPa. MPa kan worden vervangen door de eenheid N/mm², die ook de eenheid is voor buigspanning onder belasting en het dus gemakkelijker maakt om te vergelijken.

Een andere belangrijke waarde is het weerstandsmoment, dat hetzelfde is voor zowel de X- als de Y-as in onze constructieprofielen, aangezien het profielontwerp symmetrisch is. Het weerstandsmoment is altijd specifiek voor de profieldoorsnede.

De doorsnedemodulus W van onze bouwprofielen

• Bouwprofiel 20x20, groef 6: Doorsnedemodulus W_x, W_y: 0,71cm³
• Bouwprofiel 30x30, groef 8: Doorsnedemodulus W_x, W_y: 1,57cm³
• Bouwprofiel 40x40, groef 8: Doorsnedemodulus W_x, W_y: 3,58cm³

Naast de fysieke gegevens moeten we nu ook het gewicht kennen dat op het profiel werkt. We moeten ook de lengte van het profiel weten, omdat een langer profiel een hogere waarde voor de buigspanning onder dit gewicht zal laten zien dan hetzelfde profiel in een kortere versie. Tot slot spelen ook het type bevestiging en de verdeling van de belasting een rol. We hebben in de uitleg over het berekenen van de doorbuiging al duidelijk gemaakt dat deze parameters soms een aanzienlijk effect hebben op het draagvermogen van een constructieprofiel.

De buigspanning berekenen - zo doet u dat!

Parameters voor het berekenen van de buigspanning σ_b

• M Het buigmoment in N*mm van het belastingsgeval
• W Het doorsnedemodulus van de profieldoorsnede in mm³

Algemene formule voor buigspanning

${\sigma }_{\mathrm{b}}=\frac{M}{W}$

Het buigmoment M hangt af van de belasting F en de lengte L van het bouwprofiel. Of de belasting gelijkmatig verdeeld is of op één punt wordt uitgeoefend, is net zo belangrijk voor de berekening als het type bevestiging, omdat hieruit zogenaamde belastingsgevallen met verschillende formules en constante factoren voor het berekenen van het buigmoment kunnen worden afgeleid. Het buigmoment van een bepaald belastingsgeval is echter een essentieel onderdeel van de formule voor het berekenen van de buigspanning.

De belasting F is een kracht die gemeten wordt in newton (N). Dit wordt berekend door simpelweg de massa m, bijvoorbeeld het gewicht (kg), dat op het profiel werkt maal te rekenen met de gravitatieconstante g. Op aarde heeft dit een waarde van ongeveer 9,81kg*m/s ² en wordt in het gewone taalgebruik ook wel de zwaartekracht genoemd. De formule voor het omrekenen van de gewichtsbelasting F wordt in detail uitgelegd in het blogartikel over het berekenen van doorbuiging. Daar wordt de formule voor het berekenen van de oppervlaktebelasting q met gelijkmatige verdeling van de belasting in detail beschreven.

Het buigmoment M voor belastingsgevallen waarbij het profiel aan beide zijden is gemonteerd

Formule voor het buigmoment met gelijkmatige lastverdeling q

$M=\frac{q*L^2}{8}$

De formule voor het buigmoment als gevolg van gewichtsbelasting F met een gecentreerde lading

$M=\frac{F*L}{4}$

Het buigmoment M voor belastingsgevallen waarbij het profiel aan één kant is gemonteerd

Formule voor het buigmoment met gelijkmatige lastverdeling q

$M=\frac{q*L^2}{2}$

De formule voor het buigmoment als gevolg van gewichtsbelasting F aan het einde van het open profiel

$M=F*L$

Een praktisch voorbeeld van het berekenen van buigspanning

Laten we aannemen dat we een bestelwagen willen ombouwen en een bedframe willen maken van constructieprofielen op de laadvloer. Hiervoor gebruiken we constructieprofielen in 40x40mm met een groef van 8mm in een lengte van 2 meter voor de lange zijde, die aan beide zijden stevig aan de steunpalen worden bevestigd. Het verwachte gewicht dat op het profiel rust bestaat uit de som van de afzonderlijke gewichten van de matras, de lattenbodem, het beddengoed en uw eigen lichaamsgewicht. Dus we gaan hier uit van een totale massa van 100kg. We liggen normaal gesproken in bed, dus we kunnen uitgaan van een verdeelde gewichtsbelasting. Soms zitten we ook in het midden van het bed. Dit geeft ook een gemengd belastingseffect. Daarom spelen we op veilig en berekenen we hieronder de buigspanning voor een puntbelasting in het midden.

Gegeven parameters voor het berekenen van de buigspanning σ_b

• Profiel lengte L: 2.000mm
• Massa belading m: 100kg
• Doorsnedemodulus W: 3,58cm³
• Opbrengstpunt van het profiel R_e: 292MPa (or N/mm²)
• Belastinggeval Balk met gelijkmatig verdeelde belasting en steunen aan beide zijdenq

Allereerst rekenen we de massa van 100 kilogram om in kracht in newton.

$F=100\mathrm{kg}*\mathrm{9,81}\frac{m}{s^2}=981\mathrm{kg}*\frac{m}{s^2}\approx 981N$

Nu we de kracht van 981 newton weten, zullen we deze gebruiken om de verdeelde belasting te berekenen die nodig is om de buigspanning te berekenen wanneer de belasting gelijkmatig wordt uitgeoefend. We kunnen de kracht die we zojuist berekend hebben direct gebruiken voor de buigspanning wanneer de belasting in het midden wordt uitgeoefend.

$q=\frac{981N}{2.000\mathrm{mm}}=\mathrm{0,4905}\frac{N}{\mathrm{mm}}$

Uit onze berekening blijkt dat op elke millimeter van een profiel een kracht van 0,4905 newton werkt, met een kracht door gewichtsbelasting van 981 newton. We gebruiken deze waarde nu om het buigmoment te berekenen.

$M=\frac{\mathrm{0,4905}\frac{N}{\mathrm{mm}}*(2.000\mathrm{mm}{)}^2}{8}=\frac{\mathrm{0,4905}\frac{N}{\mathrm{mm}}*\mathrm{4.000.000}{\mathrm{mm}}^2}{8}=\frac{\mathrm{1.962.000}N*\mathrm{mm}}{8}=245.250N*\mathrm{mm}$

Nu de laatste stap. We berekenen de buigspanning. We moeten er hier echter ook op letten dat het vloeipunt meestal in cm wordt gegeven ³ die we moeten omrekenen naar dezelfde eenheden in mm ³. Maar dat is heel gemakkelijk, want een kubieke centimeter is 1cm*1cm*1cm of, uitgedrukt in millimeters, 10mm*10mm*10mm, wat overeenkomt met 1000mm.³.

${\sigma }_{\mathrm{b}}=\frac{245.250N*\mathrm{mm}}{\mathrm{3,58}{\mathrm{cm}}^3}=\frac{245.250N*\mathrm{mm}}{3.580{\mathrm{mm}}^3}==\mathrm{68,5055866}\frac{N}{{\mathrm{mm}}^2}$

Aangezien de waarde van de buigspanning van afgerond 68,5N/mm ² ver onder de vloeigrens van het gebruikte aluminium is, die een waarde heeft van 292N/mm ² , is er geen risico op blijvende vervorming onder een gelijkmatig verdeelde belasting van 100 kg.

Gegeven parameters voor het berekenen van de buigspanning σ_b

• Lengte profiel L: 2.000mm
• Gewichtsbelasting F: 981N
• Doorsnede modulus van profiel W: 3,58cm³
• Opbrengstpunt van het profiel R_e: 292MPa (of N/mm²)
• Belastingsgeval:Aan beide zijden ondersteunde balk met een belasting in het middenF

Hieronder berekenen we de buigspanning wanneer het gewicht als puntbelasting op dezelfde constructie werkt. Dit is het maximale type belasting dat op een aan beide zijden gemonteerd profiel kan inwerken. Voor ons voorbeeld is dit niet helemaal waar, omdat in ieder geval de lattenbodem en de matras als verdeelde belasting moeten worden gezien. Als we dat even buiten beschouwing laten, geeft het een zeer goede indicatie of de constructie blijvende schade zal oplopen door vervorming onder de belasting, of dat deze de belasting zonder problemen kan dragen.

${\sigma }_{\mathrm{b}}=\frac{981N*2000\mathrm{mm}}{4*\mathrm{3,58}{\mathrm{cm}}^3}=\frac{\mathrm{1.962.000}N*\mathrm{mm}}{4*3.580{\mathrm{mm}}^3}=\frac{\mathrm{1.962.000}N*\mathrm{mm}}{14.320{\mathrm{mm}}^3}==\mathrm{137,011173}\frac{N}{{\mathrm{mm}}^2}$

Zelfs met de belasting in het midden en met het volle gewicht van 100 kg wordt de buigspanning afgerond op 137 N/mm. ², wat lager is dan de rekgrens van het aluminiumprofiel. Pas bij een gewicht van meer dan 213 kg kan een onomkeerbare vervorming van het profiel worden verwacht op basis van de materiaaleigenschappen van de gebruikte aluminiumlegering en de profieldoorsnede..

We hopen dat de uitleg over de berekening van de buigspanning in onze constructieprofielen nuttig en gemakkelijk te begrijpen is. De formules in het artikel hebben betrekking op onze profielen, maar ze kunnen ook voor andere materialen gebruikt worden, zoals houten balken of kunststofplaten, als u de bijbehorende waarden voor de rekgrens en de doorsnedemodulus van het gewenste materiaal kent en in de formule invoert. De informatie staat meestal vermeld in de technische gegevens in het gebied van de mechanische materiaaleigenschappen in de gegevensbladen van de fabrikant.

Als u op de hoogte wilt blijven, wilt weten wat ons beweegt en wat er in onze online winkel gebeurt, volg ons dan op Instagram und Facebook. We waarderen iedere like.

Jullie Sascha van S-Polytec